Tipi visti fino a questo momento: interi e reali.
Gli oggetti sono tipi di dato composto
Ogni oggetto è rappresentato da più dati semplici.
Esempio: nella base di dati dell'Univesità ci sono i dati degli studenti.
Per ogni studente, vengono memorizzati il nome, il numero di matricola, ecc.
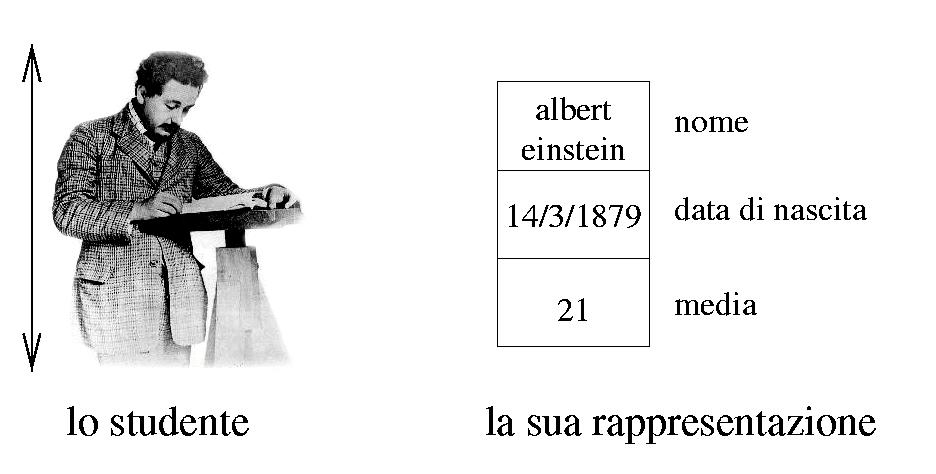
Oggetti=dati composti.
Quindi, posso rappresentare uno studente con una singola variabile.
Un punto dello schermo è rappresentato da due coordinate.
I punti sono un tipo di dato composto.
In Java, sono rappresentati come oggetti
I punti sul piano cartesiano: due variabili reali.
Lo schermo di un computer: una matrice di pixel.
Ogni pixel è dato da due coordinate intere positive.

Questa immagine, vista molto da vicino, appare:

Sono in effetti dei piccoli rettangoli colorati
Ogni rettangolo si chiama pixel
I pixel hanno coordinate e colore
Il tipo punto indica solo la posizione (le coordinate)
Le coordinate sono numeri interi
Per disegnare sullo schermo, bastano coordinate intere
Lo schermo (oppure: una finestra) si può pensare come a un reticolo.

Ogni rettangolo è un pixel.
Due coordinate intere indicano una posizione
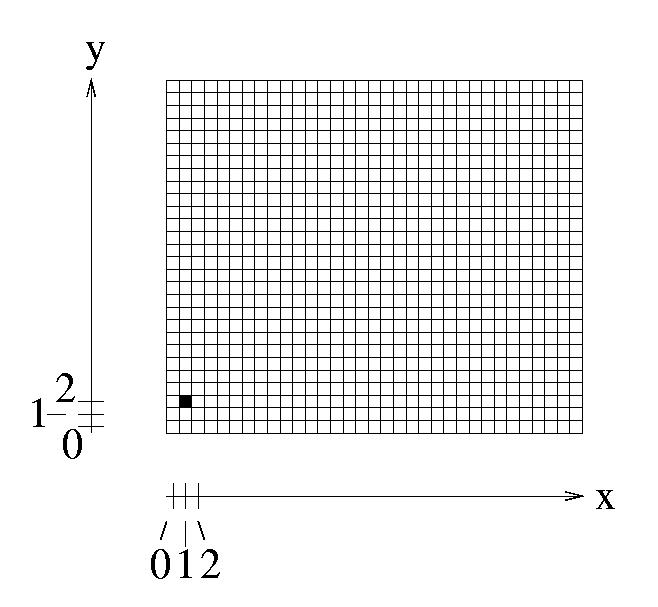
Il punto nero ha posizione (1,2).
Vediamo un tipo di dati che rappresenta una posizione
Una variabile di tipo punto rappresenta una posizione nello schermo.
Si può creare una variabile di tipo punto, nel modo seguente:
Point p;
Al contrario delle variabili intere e reali, i punti vanno creati, prima di poterli usare.
p=new Point();
Vedremo più avanti il perchè.
Ogni punto contiene due variabili intere, in cui si possono memorizzare le sue coordinate.
Se p è un punto, allora p.x e p.y sono due variabili, e si possono usare come se fossero variabili intere:
p.x=12;
p.y=3;
a=p.x+p.y;
System.out.println(p.x);
Notare che si stampa il valore numerico della coordinata (non viene disegnato il punto).
La variabile va dichiarata, e poi serve il new
Se p è dichiarata di tipo Point, allora p.x e p.y sono due variabili intere.
import java.awt.*;
class UnPunto {
public static void main(String args[]) {
Point p;
p=new Point();
int a;
p.x=12;
p.y=3;
a=p.x+p.y;
System.out.println(p.x);
}
}
La istruzione import java.awt.* serve per usare il tipo punto, e altre cose che riguardano la grafica.
È diversa da quella delle variabili.
int a; Point p; p=new Point();
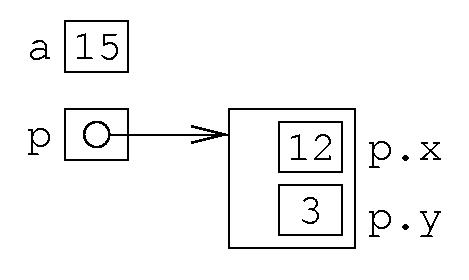
La casellina di una variabile intera contiene il suo valore.
La casellina di una variabile punto contiene un riferimento alla zona di memoria in cui si trovano p.x e p.y
In altre parole: p dice dove stanno memorizzati p.x e p.y
È come una caccia al tesoro nella memoria: la casella p non contiene l'oggetto, ma un ``biglietto'' che dice dove l'oggetto si trova.
Questo fatto per ora non ci interessa: basta aver capito che p.x e p.y sono due variabili intere.
Quando si fa:
Point p; p=new Point();
È quasi come se fosse:
// codice sintatticamente errato in Java int p.x; int p.y;
Vantaggio: uso una variabile sola per un solo punto.
In generale: una variabile rappresenta tutti i dati di qualcosa.
Esempio: si possono definire variabili per i dati degli studenti (una variabile per ogni studente), ecc.
Basta dichiarare più variabili con nomi diversi.
import java.awt.*;
class DuePunti {
public static void main(String args[]) {
Point a;
a=new Point();
Point b;
b=new Point();
a.x=12;
a.y=3;
b.x=a.y+4;
b.y=a.x+b.x;
System.out.println(b.x);
}
}
Per ogni variabile, va fatto anche il new
Per ogni punto, ho una variabile e un oggetto.
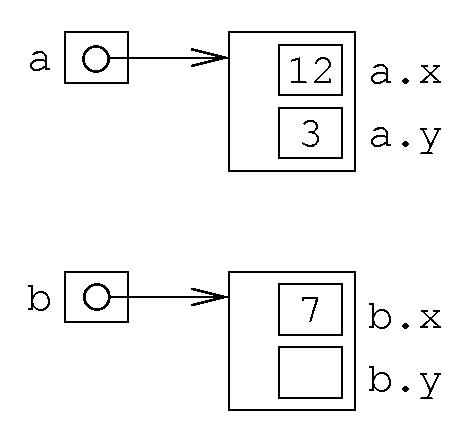
Se a, b, ecc sono variabili punto, allora a.x, a.y, b.x, b.y ecc. sono variabili intere.
I punti sono casi particolari di oggetti.
Differenza fra oggetti e valori:
Il punto è un tipo particolare di oggetti, ma ne esistono altri.
Dato un punto, trovare la distanza dall'origine
import java.awt.*;
class Distanza {
public static void main(String args[]) {
Point p;
p=new Point();
p.x=10;
p.y=20;
...
}
}
Completare il programma, in modo che stampi la distanza.
Serve una variabile reale
Le coordinate sono p.x e p.y
La distanza si calcola come al solito.
import java.awt.*;
class Distanza {
public static void main(String args[]) {
Point p;
p=new Point();
p.x=10;
p.y=20;
double dis;
dis=Math.sqrt(p.x*p.x+p.y*p.y);
System.out.println(dis);
}
}
Vista prima: un dato <--> più dati.
Altra differenza: i metodi.
Esempio: spostare un punto.
p.translate(10,-20);
Il punto p viene spostato di 10 sulla coordinata x e di -20 sulla coordinata y.
Muove il punto alle coordinate specificate.
p.move(5, 14);
Equivale alle due istruzioni:
p.x=5; p.y=14;
Notare:
In generale: ci sono molti modi per fare una cosa, e ci sono metodi che equivalgono a molte istruzioni.
Programma della distanza, con il metodo move per definire il punto.
import java.awt.*;
class Distanza {
public static void main(String args[]) {
Point p;
p=new Point();
p.move(10,20);
double dis;
dis=Math.sqrt(p.x*p.x+p.y*p.y);
System.out.println(dis);
}
}
Vantaggi di usare il metodo invece dei due assegnamenti.
La seconda cosa è importante in programmi lunghi
Spostare un punto di 10 unità a destra, e calcolare la distanza dall'origine.
import java.awt.*;
class Sposta {
public static void main(String args[]) {
Point p;
p=new Point();
p.move(23,42);
...
}
}
Mettere delle istruzioni al posto di ... in modo che venga spostato il punto e calcolata la nuova distanza.
Primo: si sposta il punto usando il metodo translate
Secondo: si calcola la distanza come visto prima.
import java.awt.*;
class Sposta {
public static void main(String args[]) {
Point p;
p=new Point();
p.move(23,42);
p.translate(10,0);
double dis;
dis=Math.sqrt(p.x*p.x+p.y*p.y);
System.out.println(dis);
}
}
Completare questo programma:
deve stampare la distanza fra i due punti.
import java.awt.*;
class DistDue {
public static void main(String args[]) {
Point a;
a=new Point();
Point b;
b=new Point();
a.move(12,32);
b.move(3,90);
...
}
}
Suggerimento: una espressione può anche contenere più parentesi tonde, per esempio:
var=(10+(20-1)*2)*8
Non si possono invece usare parentesi quadre [] oppure graffe {} all'interno delle espressioni (perchè hanno un significato diverso).
Basta usare la formula della distanza.
Le coordinate sono date da a.x ecc
import java.awt.*;
class DistDue {
public static void main(String args[]) {
Point a;
a=new Point();
Point b;
b=new Point();
a.move(12,32);
b.move(3,90);
double dis;
dis=Math.sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
System.out.println(dis);
}
}
Se a e b sono interi, allora a=b copia il valore di b in a.
Se a e b sono punti (oppure altri oggetti), allora è "sbagliato":
a=b;
Vedremo perchè non va usato questo sistema, e quando si può invece usare.
Per il momento, diciamo che non va usato.
Si fa la copia componente per componente:
Point a, b; ... a.x=b.x; a.y=b.y;
Dati i tre punti di un triangolo, calcolare il suo perimetro.
import java.awt.*;
class Perim {
public static void main(String args[]) {
Point a;
a=new Point();
Point b;
b=new Point();
Point c;
c=new Point();
a.move(10,10);
b.move(15,10);
c.move(30,20);
...
}
}
Per ogni coppia di punti, calcolo la distanza (la lunghezza del lato).
Le sommo, e ottengo il perimetro.
import java.awt.*;
class Perim {
public static void main(String args[]) {
Point a;
a=new Point();
Point b;
b=new Point();
Point c;
c=new Point();
a.move(10,10);
b.move(15,10);
c.move(30,20);
double lato1, lato2, lato3;
lato1=Math.sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
lato2=Math.sqrt((b.x-c.x)*(b.x-c.x)+(b.y-c.y)*(b.y-c.y));
lato3=Math.sqrt((c.x-a.x)*(c.x-a.x)+(c.y-a.y)*(c.y-a.y));
double perimetro;
perimetro=lato1+lato2+lato3;
System.out.println(perimetro);
}
}
Faccio più volte la stessa cosa (calcolo la distanza fra due punti)
Esiste un modo per non scrivere il codice più volte (settimana prossima).
Dati i tre punti, trovare l'area del triangolo.
import java.awt.*;
class Area {
public static void main(String args[]) {
Point a;
a=new Point();
Point b;
b=new Point();
Point c;
c=new Point();
a.move(10,10);
b.move(15,10);
c.move(30,20);
...
}
}
Sono possibili varie soluzioni.
Quella più facile: usare la formula di Erone
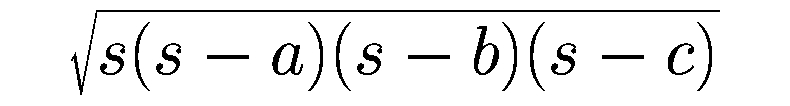
Dove a, b e c sono i latui.
È facile perchè sappiamo come calcolare i lati a, b e c, e anche come calcolare s, che è la metà del perimetro.
Il modo migliore di risolvere un problema è quello di adattare/combinare soluzioni già note.
import java.awt.*;
class Area {
public static void main(String args[]) {
Point a;
a=new Point();
Point b;
b=new Point();
Point c;
c=new Point();
a.move(10,10);
b.move(15,10);
c.move(30,20);
double lato1, lato2, lato3;
lato1=Math.sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
lato2=Math.sqrt((b.x-c.x)*(b.x-c.x)+(b.y-c.y)*(b.y-c.y));
lato3=Math.sqrt((c.x-a.x)*(c.x-a.x)+(c.y-a.y)*(c.y-a.y));
double semiperimetro;
semiperimetro=(lato1+lato2+lato3)/2;
double area;
area=Math.sqrt(semiperimetro*(semiperimetro-lato1)*
(semiperimetro-lato2)*(semiperimetro-lato3));
System.out.println(area);
}
}
Un rettangolo è dato dai seguenti dati:
Queste sono le variabili di cui è fatto un rettangolo.
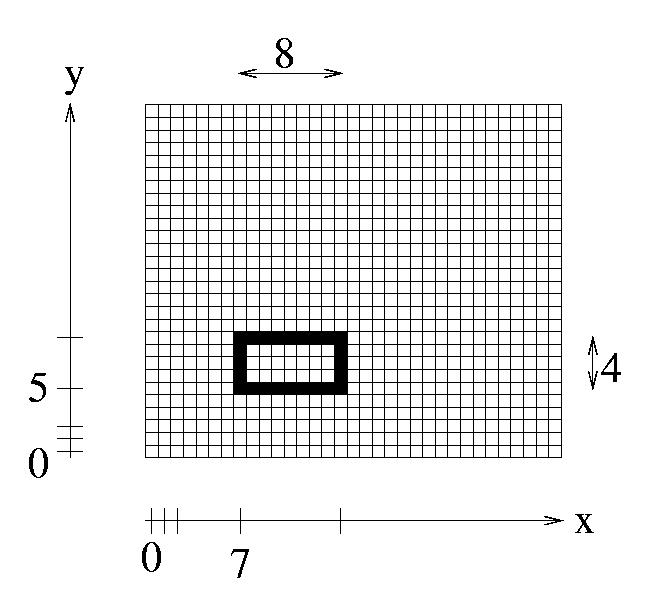
In questo caso, x=7, y=5, width=8 e height=4
Questo programma definisce un rettangolo.
import java.awt.*;
class Rettan {
public static void main(String args[]) {
Rectangle r;
r=new Rectangle();
r.x=12;
r.y=10;
r.width=5;
r.height=4;
}
}
r.x ecc sono variabili intere
Completare il programma qui sotto in modo che stampi l'area del rettangolo.
import java.awt.*;
class Rettan {
public static void main(String args[]) {
Rectangle r;
r=new Rectangle();
r.x=12;
r.y=10;
r.width=5;
r.height=4;
...
}
}
Dal momento che i due lati sono r.width ed r.height...
import java.awt.*;
class Rettan {
public static void main(String args[]) {
Rectangle r;
r=new Rectangle();
r.x=12;
r.y=10;
r.width=5;
r.height=4;
int area;
area=r.width*r.height;
System.out.println(area);
}
}
Ogni rettangolo ha la parte x, y, height e width
I punti hanno soltanto x e y
Ci sono altri tipi di oggetti che hanno parti diverse da queste.
Per i rettangoli esiste il metodo setSize (che modifica altezza a larghezza)
Per i punti questo metodo non esiste
Ogni tipo di oggetto (Point, Rectangle, ecc) ha i suoi metodi.
Qualche metodo:
Trovare la diagonale di un rettangolo.
import java.awt.*;
class Diago {
public static void main(String args[]) {
Rectangle r;
r=new Rectangle();
r.setBounds(10,20,4,6);
...
}
}
Il metodo setBounds cambia i valori delle componenti del rettangolo.
Sono noti i due lati...
import java.awt.*;
class Diago {
public static void main(String args[]) {
Rectangle r;
r=new Rectangle();
r.setBounds(10,20,4,6);
double d;
d=Math.sqrt(r.width*r.width+r.height*r.height);
System.out.println(d);
}
}
Aumentare le dimensioni di un rettangolo in modo che includano un certo punto.
Usare il metodo grow(n,m) che aumenta la dimensione di un rettangolo di n in tutte e quattro le dimensioni, mantenendo il centro (ossia, aumenta di 2n e 2m la base e l'altezza).
Il metodo Math.abs calcola il valore assoluto di un numero.
La larghezza va aumentata in modo tale che la larghezza del rettangolo sia il doppio della distanza fra il centro e il punto da includere.
import java.awt.*;
class Aumenta {
public static void main(String args[]) {
Rectangle r;
r=new Rectangle();
r.setBounds(5,5,8,10);
Point p;
p=new Point();
p.move(20,20);
Point centro;
centro=new Point();
centro.move(r.x+r.width/2, r.y+r.height/2);
r.grow(Math.abs(p.x-centro.x-r.width), Math.abs(p.y-centro.y-r.height));
System.out.println(r.toString());
}
}
Nota: se grow(n,m) aumenta la distanza fra il centro e i vertici di n ed m nelle due direzioni.
Il metodo toString converte un oggetto in stringa.
Nota: vengono stampati i valori dell'oggetto (nel nostro caso, x, y, width e height) e non viene disegnato il rettangolo.
Osservazione: si possono anche definire degli oggetti per memorizzare dati temporanei (in questo caso, il centro del rettangolo)